Status of this Document
This section describes the status of this document at the time of its publication. Other documents may supersede this document. A list of current W3C publications and the latest revision of this technical report can be found in the W3C technical reports index at http://www.w3.org/TR/.
This Note is a self-contained discussion of Arabic mathematical notation in
MathML. It provides guidelines for the handling of Arabic mathematical
presentation using MathML 2
Recommendation (2nd Edition) [MathML22e]
and suggests extensions for a future revision.
This Note has been written by participants in the Math Interest Group (W3C
members only) which is part of the W3C Math activity. Please direct
comments and report errors in this document to www-math@w3.org, a mailing list with a public archive.
Publication as a Interest Group Note does not imply endorsement by the W3C Membership. This is a draft document and may be updated, replaced or obsoleted by other documents at any time. It is inappropriate to cite this document as other than work in progress.
1 Introduction
As the World Wide Web becomes more world wide, inclusion of the world's many languages,
scripts and cultures becomes critical. Although the development of the Mathematical
Markup Language (MathML) [MathML22e], was neither intentionally nor
explicitly exclusive of non-European languages and scripts,
the focus was on the notational schema used with European languages. Indeed, most of these
notations are used unchanged in many other contexts. However, there are variations introduced
in some languages, either for historical reasons, or to fit within various writing systems,
which MathML should accommodate for improved international support (in particular educational
material requiring these variations, or historical documents).
While European languages are written left to right (LTR), Arabic, among others, is
written right to left (RTL). We will see that in Arabic mathematical texts many of the
same notational constructs are used, but may be reversed or mirrored,
depending on the cultural context; what we will call a mathematical directionality.
The mathematical directionality is not necessarily the same as the text directionality.
Moreover, since the mathematical material may commonly contain text and symbols coming from
both Arabic and European languages, the question of how the Unicode bidirectional algorithm
[UnicodeBiDi] should be applied arises.
Finally, several additional symbols and writing styles may be used in special ways.
![[Arabic Script samples]](arabic-images/khtout.png)
Arabic Calligraphy is enriched by a variety of writing styles,
as European writing benefits from a variety of fonts. The graphic above illustrates
a variety of Arabic calligraphic styles; each word is the name of the corresponding style.
In the same way that European mathematics broadens the set of distinct symbols available by
using bold face, Fraktur or other styles, so does Arabic mathematics but typically
by varying strokes, adding tails or other extensions.
A given piece of mathematics marked up in
Content MathML
([MathML22e], chapter 4), is generally language-neutral — although the
choices for variable names may imply a cultural context —
it intends to represent the universal meaning of the mathematics.
A given piece of mathematics marked up in
Presentation MathML
([MathML22e], chapter 3),
on the other hand, conveys the visual appearance of the expression. That appearance
necessarily targets a specific language and notational conventions, indeed even of
the scientific discipline involved.
In this Note, we amplify and formalize this segregation of concerns:
Presentation MathML should be a fairly literal
representation of the visual notation to be used.
We relegate all localization issues
— which symbol to use for summation, which name to use for tangent, what
format to use for numbers — to the generator of the Presentation MathML,
rather than the renderer. This avoids guessing, perhaps wrongly, what number is
intended while deciding whether to replace periods by commas, for example. Thus,
localization entails the choice of what
text content to place within MathML's token elements, but that choice is already fixed
within a given piece of Presentation MathML.
In this Note, we have attempted to examine all notational conventions in current
use with Arabic and languages written using Arabic script, without giving preference
to one form over another.
We aim to clarify the specification of MathML, proposing extensions where needed,
so that MathML has the broadest coverage possible. Nevertheless, an in-depth analysis of issues
affecting other languages, particularly those written top to bottom is a topic for future study.
The emphasis on Arabic languages is partly a reflection of an increased interest in, and
usage of, MathML in Arabic language contexts that have highlighted the issues described here.
Another topic for future study is how Content MathML might best support the transformation
to appropriately localized Presentation MathML.
2 Some Features of Arabic Script
Before delving into mathematical notations, it will help to describe some
of the features of Arabic script, and how Unicode deals with these features.
2.1 Text Direction
While European languages are written from left to right (LTR), Arabic is written from
right to left (RTL). Unicode supports these scripts by not only defining codepoints
for the individual characters of these languages, but by recording the directionality
of each character.
When a mixture of LTR and RTL characters appear in text (ie. bidirectional or BiDi text,
such as an English text that includes Arabic words),
Unicode's bidirectional algorithm [UnicodeBiDi] describes the order in which
the characters will be displayed. All adjacent strongly-typed RTL characters (such as a
in a single Arabic word) will be presented in right-to-left order, and vice versa for
strongly-typed LTR characters. A cluster of characters with the same directionality
is called a directional run.
Within any given "paragraph", directional runs are then ordered according to the
overall directional context. The bidirectional algorithm allows for higher-level
protocols to determine which segments of a structured text constitute "paragraphs"
in this sense. For example, in HTML block-level elements are taken as the
paragraph segments. The top-level html tag determines the directional context
which can be changed on lower-level elements using the dir attribute.
For a gentle introduction to bidirectional text, see
[UnicodeBiDiIntro].
2.2 Glyph Shaping
As Arabic is a calligraphic script, letters within words are typically joined together.
When text in such calligraphic scripts is specified by character sequences, a
process called shaping is used to blend, or connect the character glyphs.
In Arabic words consisting of a single character, that character is drawn in the "isolated"
style. In multi-character words, alternative shapes are generally used depending on position:
the first (rightmost) character is drawn in its "initial" shape,
the last (leftmost) character gets its "final" shape, and any characters in the middle
are of the "medial" shape.
Compare the isolated characters غ ي ر
to the result of glyph shaping غير.
2.3 Mirroring
Some characters, viewed abstractly, have the same meaning in many languages,
but the form used in RTL languages are the roughly the mirror image of the
form used in LTR languages. Parentheses and quotation marks are such characters.
Unicode deals with these cases by marking some codepoints as mirrored, meaning
that an alternate glyph will be used for the character if it appears in a RTL context.
Note that mirrored symbols are not required by Unicode (See
Mirroring
in [UnicodeBiDi], section 6) to be literally
the exact mirror image. Indeed, it is considered an important point of Arabic calligraphy
that they are not: the feather's head (kalam) is a flat rectangle. The writer holds the pen so that
the largest side makes an angle of approximately 70° with the baseline.
This orientation is kept throughout the process of drawing the character.
Furthermore, as Arabic writing goes from right to left, some boldness is produced
around segments running from top left toward the bottom right and conversely,
segments from top right to the bottom left will rather be slim.
Thus, the Arabic sum symbol 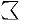 ,
for example, is not simply the mirror image
,
for example, is not simply the mirror image
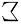 of sigma
of sigma 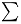 .
.
2.4 Number Systems
There are several decimal numeral systems in use in Arabic:
| System | Unicode | Digits | Image | Regions |
|---|
| European | U0030-U0039 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | Maghreb Arab (eg. Morocco), as well as European |
|---|
| Arabic-Indic | U0660-U0669 | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ | ![[Image of Arabic-Indic Digits]](arabic-images/arind.png) | Machrek Arab (eg. Egypt) |
|---|
| Eastern Arabic-Indic | U06F0-U06F9 | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ![[Image of Eastern Arabic-Indic Digits]](arabic-images/esarind.png) | Iran |
|---|
3 Comparison of Mathematical Notations
We will explore the spectrum of notations by choosing some samples of mathematical
content and comparing how they would typically be rendered for different languages and cultures.
We begin with an expression formatted as it might be seen in both English
and French contexts.
| Style | Image | MathML |
|---|
| English | ![[Image of formula in English style]](arabic-images/expren.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> if </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> if </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">S</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tan</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> otherwise </mtext>
<mrow>
<mo>(</mo>
<mtext>with </mtext>
<mi>π</mi>
<mo>≃</mo>
<mn>3.141</mn>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
| French | ![[Image of formula in French style]](arabic-images/exprfr.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> si </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> si </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">E</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tg</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext> sinon </mtext>
<mrow>
<mo>(</mo>
<mtext>avec </mtext>
<mi>π</mi>
<mo>≃</mo>
<mn>3,141</mn>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
Structurally, the expressions are identical. The differences in names,
number formatting and of course the language used for the connecting words are all
due to localization. They are effected purely by
differing textual content within the MathML token elements.
In the following sections, we will examine three common styles used
for mathematics within Arabic texts. The terms Moroccan, Maghreb and Machrek will be
used to indicate the general geographic areas where these styles are used, but
there are no clearly defined borders between the regions.
3.1 Arabic Notation; Moroccan Style
The current way of writing mathematical expressions in Morocco,
is closely related to the French style:
| Style | Image | MathML |
|---|
| Moroccan | ![[Image of formula in Moroccan style]](arabic-images/exprfrm.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>إذاكان </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>إذاكان </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">E</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tg</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>غيرذلك </mtext>
<mrow>
<mo>(</mo>
<mi>π</mi>
<mo>≃</mo>
<mn>3,141</mn>
<mtext>مع</mtext>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
Although the mathematics would be embedded within a RTL language (Arabic),
its directionality is still LTR. The connecting words and phrases within the math, however,
are RTL Arabic, and should be subject to glyph shaping
(although some current MathML renderers are not doing this).
Thus these phrases should appear as
"إذاكان" (for "if"),
"غيرذلك" (for "otherwise")
and "مع" (for "with").
Also, the indication is that the bidirectional algorithm [UnicodeBiDi] should be
applied to individual text and token elements, rather than at a higher level as in HTML;
that is, the token elements act as paragraph segments.
Even with these considerations, the ordering of phrases within the last clause
(for "otherwise (with pi=3.141)") is problematic. The obvious markup sandwiching
an mrow for "pi=3.141" between two mtext's for "otherwise (with" and ")", respectively,
would yield an incorrect ordering. A correct rendering seems to require the possibility
of embedding math within mtext, which is not possible in MathML 2.0.
But even then, the desired ordering would need to be marked up as two separate mtext elements:
one for "otherwise", and one for "(with pi=3.141)". The Math Interest Group is currently
considering the possibilities of such embedding. The example above was marked up by
artificially placing the Arabic word for "with" after the "pi=3.141".
Given such issues, it is sometimes advantageous to minimize the use of
connecting phrases, with preference to simple punctuation, such as:
| Style | Image | MathML |
|---|
| Moroccan | ![[Image of simplified formula in Moroccan style]](arabic-images/exprfrn.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<mi>f</mi>
<mo></mo>
<mrow>
<mo>(</mo>
<mi>x</mi>
<mo>)</mo>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mo>{</mo>
<mtable>
<mtr>
<mtd>
<mrow>
<munderover>
<mo movablelimits="false">∑</mo>
<mrow>
<mi>i</mi>
<mo>=</mo>
<mn>1</mn>
</mrow>
<mi>s</mi>
</munderover>
<mo></mo>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>; </mtext>
<mi>x</mi>
<mo><</mo>
<mn>0</mn>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>s</mi>
</msubsup>
<mo></mo>
<mrow>
<msup>
<mi>x</mi>
<mi>i</mi>
</msup>
<mo></mo>
<mi>d</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>; </mtext>
<mi>x</mi>
<mo>∈</mo>
<mi mathvariant="normal">E</mi>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mi>tg</mi>
<mo></mo>
<mi>π</mi>
</mrow>
</mtd>
<mtd>
<mrow>
<mtext>; </mtext>
<mrow>
<mo>(</mo>
<mi>π</mi>
<mo>≃</mo>
<mn>3,141</mn>
<mo>)</mo>
</mrow>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</mrow>
</math>
|
|---|
3.2 Arabic Notation; Maghreb Style
The Maghreb style of notation is widely used in North Africa:
| Style | Image | MathML |
|---|
| Maghreb | ![[Image of formula in Maghreb style]](arabic-images/exprare.png) | Not yet attempted |
|---|
Here, the most striking difference is that the overall mathematical
layout is the mirror image of the preceding examples, that is,
the mathematical directionality is RTL. Further, some symbols
(eg ∑, <, ∈) are mirrored as well.
Thus, we need a means of specifying the mathematical directionality,
and assuring that the appropriate symbols are available in Unicode and are marked as mirrored.
The remaining differences are due to a more pronounced use of Arabic symbols:
DAL 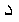 (as the initial
of
(as the initial
of 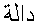 = "function" in Arabic);
the Arabic letter BEH
= "function" in Arabic);
the Arabic letter BEH 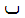 ,
and the letters of the function name abbreviation
,
and the letters of the function name abbreviation 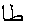 for tangent (without dots). Again, these differences fall into the category of localization,
but reinforce the idea that the Unicode bidirectional algorithm, along with glyph shaping, should apply individually
to token elements.
for tangent (without dots). Again, these differences fall into the category of localization,
but reinforce the idea that the Unicode bidirectional algorithm, along with glyph shaping, should apply individually
to token elements.
3.4 Additional Arabic Notations
Two additional unique notations involve combinatorics, namely the factorial and
binomial coefficients:
| Style | Image | MathML |
|---|
| English | ![[Image of 12 factorial in english style]](arabic-images/drbcen.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow><mn>12</mn><mo>!</mo></mrow>
</math>
|
|---|
| Arabic | ![[Image of 12 factorial in Arabic style]](arabic-images/drbc.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block" dir="rtl">
<menclose notation="madruwb">
12
</menclose>
</math>
|
|---|
The argument to the factorial must be wrapped in a form similar to the
character LAM (ل), which must
be stretched in both directions to accommodate. A new menclose notation,
madruwb is proposed for this case.
| Style | Image | MathML |
|---|
| English | ![[Image of binomial(5,12) in english style]](arabic-images/arrangaen.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mo>(</mo><mtable><mtr><mtd>5</mtd></mtr><mtr><mtd>12</mtd></mtr></mtable><mo>)</mo>
</mrow>
</math>
|
|---|
| Arabic | ![[image of binomial(5,12) in Arabic style]](arabic-images/arranga.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block" dir="rtl">
<mmultiscripts><mo>ل</mo>
<mn>12</mn><none/>
<mprescripts/>
<none/><mn>5</mn>
</mmultiscripts>
</math>
|
|---|
Finally, although stacked fractions are rendered the same way in both European and Arabic,
bevelled fractions in RTL Arabic will appear, as one would expect, with the terms in RTL order,
i.e. A divided by B would appear as "B/A".
In some locales, the preference is for the slash to also be mirrored, as "B\A". For these cases,
we suggest that authors employ explicit markup using the REVERSE SOLIDUS \, such as
<mrow><mi>A</mi><mo>\</mo><mi>B</mi></mrow>
.
3.5 Persian
Persian languages generally use the Arabic script (written RTL), but with
the mathematical directionality LTR, similar to the Moroccan style.
We are aware of only one mathematical notation unique to Persian writing, the notation used
for limits:
| Style | Image | MathML |
|---|
| English | ![[Image of limit formula in English style]](arabic-images/limw.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<munder>
<mo movablelimits="false">lim</mo>
<mrow>
<mi>x</mi>
<mo>→</mo>
<mfrac bevelled="true">
<mi>π</mi>
<mn>10</mn>
</mfrac>
</mrow>
</munder>
<mo></mo>
<mrow>
<mi>sin</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mfrac>
<mn>1</mn>
<mn>4</mn>
</mfrac>
<mo></mo>
<mrow>
<mo>(</mo>
<msqrt>
<mn>5</mn>
</msqrt>
<mo>-</mo>
<mn>1</mn>
<mo>)</mo>
</mrow>
</mrow>
</mrow>
</math>
|
|---|
| Persian | ![[Image of limit formula in Persian style]](arabic-images/limf.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block">
<mrow>
<mrow>
<munder>
<mo movablelimits="false">حد</mo>
<mrow>
<mi>x</mi>
<mo>→</mo>
<mfrac bevelled="true">
<mi>π</mi>
<mn>۱۰</mn>
</mfrac>
</mrow>
</munder>
<mo></mo>
<mrow>
<mi>sin</mi>
<mo></mo>
<mi>x</mi>
</mrow>
</mrow>
<mo>=</mo>
<mrow>
<mfrac>
<mn>۱</mn>
<mn>۴</mn>
</mfrac>
<mo></mo>
<mrow>
<mo>(</mo>
<msqrt>
<mn>۵</mn>
</msqrt>
<mo>-</mo>
<mn>۱</mn>
<mo>)</mo>
</mrow>
</mrow>
</mrow>
</math>
|
|---|
While the overall notation is similar to the Moroccan model (LTR), it uses the
Eastern Arabic-Indic digits. The word "حد" (for "limit"), is
used; this word should not only be affected by glyph shaping,
but should be stretched horizontally to match the length of the underscript.
4 Proposals and Clarifications
4.1 Clarification of bidirectional Algorithm for MathML
The following summarizes how directionality should be applied to MathML
and, in particular, describes how the bidirectional algorithm should be applied
(it falls into class HL4; See Higher Level
Protocols: HL4 in [UnicodeBiDi], section 4.3).
The overall mathematical directionality should be determined by
a (new) dir attribute on the outermost math element
which takes one of the values ltr or rtl;
the default is ltr.
If this attribute is rtl the layout of all Layout, Script, Limit,
Table and Matrix schemata should proceed from right to left. This includes
such effects as the surd of an mroot starting from the right.
When the mathematical directionality is ltr, the layout should conform
to the current MathML specification.
The text content of each Token element should be treated as a separate
directional segment and the bidirectional algorithm should be applied to each independently.
The initial directional context for each Token element is determined
by the mathematical directionality. This latter property should assure that
individual mirrored symbols are treated correctly.
As an example, consider the MathML fragment:
<mn>1</mn>
<mo>+</mo>
<mi>
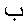 </mi>
<mo>-</mo>
<mn>2</mn>
</mi>
<mo>-</mo>
<mn>2</mn>
Some browsers mis-apply the bidirectional algorithm to the expression as a whole, as in HTML.
Applying the HTML algorithm would set the first two items LTR, but then switch directions upon
encountering the letter 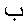 ;
thus the last three items are reversed.
;
thus the last three items are reversed.
| Style | Image | MathML |
|---|
| Right | ![[Image of expression rendered correctly]](arabic-images/direction1.png) |
<math xmlns="http://www.w3.org/1998/Math/MathML" display="display">
<mn>1</mn><mo>+</mo><mi>ب</mi><mo>-</mo><mn>2</mn>
</math>
|
|---|
| Wrong | ![[Image of expression rendered incorrectly]](arabic-images/direction2.png) | |
|---|
4.2 Glyph Shaping
Glyph shaping rules apply not only to the textual content of an mtext,
but also to Arabic character sequences used as mathematical symbols (particularly in
mi and mo). This shaping is the visual cue that
distinguishes a single symbol from a sequence of symbols, perhaps representing a product.
This is analogous to the use of roman font in European mathematics, to distinguish for example
<math xmlns="http://www.w3.org/1998/Math/MathML" display="display"><mi>sin</mi></math>
from
<math xmlns="http://www.w3.org/1998/Math/MathML" display="display"><mi>s</mi><mi>i</mi><mi>n</mi></math>
.
Thus, implementors should apply shaping to each character sequence within the text content of
any token elements.
Certain Arabic characters (ا د ذ ر ز و)
have no unique initial or medial shapes. Their use in the middle of a mathematical symbol
would tend to make the symbol look like the product of two shorter symbols.
Thus, to avoid confusion, authors should avoid using these characters
in the middle of mathematical symbols.
4.3 Additional Mathvariants
For single character tokens, additional styles, besides isolated, are used
to enlarge the set of available distinct symbols, just as the bold and Fraktur styles are
used in European mathematics. The styles used in Arabic mathematics
are "tailed", "looped" and "stretched", in addition to the "initial" style applied to
the individual character. Furthermore, the "double-struck" style is commonly used.
The following table shows the character JEEM in the various styles, in both
dotted and undotted forms (see below):
| isolated | initial | tailed | looped | stretched | double-struck |
|---|
| dotted | 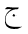 |  |  | 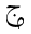 |  |  |
|---|
| undotted | 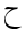 | 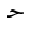 | 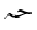 | 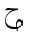 | 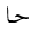 |  |
|---|
It is proposed to consider the mathvariant "normal",
when applied to Arabic, to mean the result of glyph shaping, and in particular,
the "isolated" style for single character tokens. It is also proposed to
add the following values allowed for mathvariant:
"initial", "tailed", "looped" and "stretched".
It is not expected to be meaningful to apply the "bold", "italic", "fraktur", "script",
"sans-serif" or "monospace" mathvariants (or combinations) to Arabic (although there is some
sentiment for allowing "bold" and "italic"). Nor is it meaningful to apply any mathvariant
other than "normal" to multicharacter tokens, which should have glyph shaping applied.
The current MathML specification points out that the only combinations of characters and
mathvariant that have an unambiguous interpretation are those that correspond to the
SMP Math Alphanumeric Symbols. An analogous argument is to be made for Arabic and the proposed
Arabic Math Alphabetic Symbols [UnicodeProposition] (not yet part of Unicode).
Both dotted and undotted alphabetic symbols are encountered in this Note.
The choice of which type to use is up to local preferences, however; documents use
either dotted or undotted symbols, but not a mixture, and in particular, the dots are not used
to indicate semantic distinctions. Thus, it is not felt that dotting is a good
candidate for a mathvariant value, but rather should be accommodated by the choice of
symbol fonts available to user's browser, or possibly through CSS.
4.4 Mirroring
The MathML attributes lspace, rspace,
lquote and rquote should be interpreted as opening and closing,
rather than strictly left and right. This historical anomaly is analogous to
the standard Unicode names for the parentheses:
The LEFT PARENTHESIS and RIGHT PARENTHESIS
are marked as mirrored and are taken to represent
OPENING PARENTHESIS and CLOSING PARENTHESIS, respectively.
The Math Working Group, and other interested parties, should work to assure
that the necessary codepoints for Arabic mathematics are not only available, but
appropriately marked for mirroring.
It is also to be hoped that available fonts will be available, and will
respect the calligraphic qualities regarding mirroring.
4.5 Horizontal Stretchiness
In Arabic mathematics, the sum, product and limit are commonly stretched horizontally
to the same width as the limits (over or under) that apply to them. Such stretching
does occasionally appear, but is rare, in European mathematics.
In Horizontal
Stretching Rules of MathML
([MathML22e] section 3.2.5.8.3), standard allows for such horizontal stretching
of some symbols at the discretion of the rendering agent. In this Note, we
simply encourage developers to implement this feature for the appropriate Arabic symbols.
4.6 Additional Constructs
The Arabic notation for factorial is a sort of enclosure.
We propose to add an additional allowed value madruwb (transliteration
of the Arabic مضروب for factorial) for
the notation attribute of menclose.
5 Conclusions and Future Work
This Note describes the notational issues encountered in presenting
mathematics within Arabic and other RTL languages, in particular focusing on
how these notations differ from the model described by MathML2. To the best of
our knowledge, the unique notations described here cover all known differences.
This Note also proposes enhancements to be considered in a future revision
of the MathML specification. These enhancements would allow Presentation MathML to be
used to conveniently incorporate mathematics into Arabic documents in a style
conventionally used by Arabic speaking authors.
The successful use of mathematics in Arabic texts will also require,
in addition to the extensions proposed here, that the appropriate codepoints
are included in Unicode, and that those codepoints are correctly marked as
mirrored. Some proposals ([UnicodeProposition],[ArabicMathUnicode]) have already been made.
6 Acknowledgments
This document has been produced by the members of the Math Interest
Group. The chairs of this Interest Group are David Carlisle (invited
expert) and Robert Miner (Design Science, Inc.). Other members of the
Working Group are (at the time of writing): Isam Ayoubi (invited
expert), Laurent Bernardin (Waterloo Maple Inc.), Stephane Dalmas
(Institut National de Recherche en Informatique et en Automatique),
Stan Devitt (invited expert), Max Froumentin (W3C), Patrick D F Ion
(invited expert), Azzeddine LAZREK (invited expert), Paul Libbrecht
(German Research Center for Artificial Intelligence), Manolis Mavrikis
(University of Edinburgh), Bruce Miller (National Institute of
Standards and Technology), Luca Padovani (University of Bologna), Neil
Soiffer (Design Science, Inc.), Stephen Watt (Waterloo Maple Inc.)
The editors would also like to thank Richard Ishida for initiating
the contacts that lead to the writing of this Note, and for many
constructive comments on a draft of it.
7 Production Notes
The images of Arabic and Persian expressions were composed using the RyDArab
system [RyDArab], and the FarsiTeX system [FarsiTeX], respectively.
![[Arabic Script samples]](arabic-images/khtout.png)
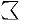 ,
for example, is not simply the mirror image
,
for example, is not simply the mirror image
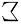 of sigma
of sigma 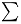 .
.![[Image of Arabic-Indic Digits]](arabic-images/arind.png)
![[Image of Eastern Arabic-Indic Digits]](arabic-images/esarind.png)
![[Image of formula in English style]](arabic-images/expren.png)
![[Image of formula in French style]](arabic-images/exprfr.png)
![[Image of formula in Moroccan style]](arabic-images/exprfrm.png)
![[Image of simplified formula in Moroccan style]](arabic-images/exprfrn.png)
![[Image of formula in Maghreb style]](arabic-images/exprare.png)
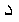 (as the initial
of
(as the initial
of 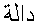 = "function" in Arabic);
the Arabic letter BEH
= "function" in Arabic);
the Arabic letter BEH 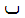 ,
and the letters of the function name abbreviation
,
and the letters of the function name abbreviation 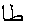 for tangent (without dots). Again, these differences fall into the category of localization,
but reinforce the idea that the Unicode bidirectional algorithm, along with glyph shaping, should apply individually
to token elements.
for tangent (without dots). Again, these differences fall into the category of localization,
but reinforce the idea that the Unicode bidirectional algorithm, along with glyph shaping, should apply individually
to token elements.![[Image of formula in Machrek style]](arabic-images/exprarw.png)
 is used for the summation
(initial of
is used for the summation
(initial of 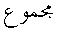 = "sum" in Arabic);
a different letter
= "sum" in Arabic);
a different letter  is used for the function
(initial of
is used for the function
(initial of  , also "function" in Arabic);
the letters of the elementary function name abbreviation
, also "function" in Arabic);
the letters of the elementary function name abbreviation
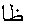 are with dots;
and a number format using Arabic-Indic digits and a comma for the decimal separator (but not
the same as the Arabic comma used in text).
are with dots;
and a number format using Arabic-Indic digits and a comma for the decimal separator (but not
the same as the Arabic comma used in text).![[Image of 12 factorial in english style]](arabic-images/drbcen.png)
![[Image of 12 factorial in Arabic style]](arabic-images/drbc.png)
![[Image of binomial(5,12) in english style]](arabic-images/arrangaen.png)
![[image of binomial(5,12) in Arabic style]](arabic-images/arranga.png)
![[Image of limit formula in English style]](arabic-images/limw.png)
![[Image of limit formula in Persian style]](arabic-images/limf.png)
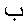 </mi>
<mo>-</mo>
<mn>2</mn>
</mi>
<mo>-</mo>
<mn>2</mn>
![[Image of expression rendered correctly]](arabic-images/direction1.png)
![[Image of expression rendered incorrectly]](arabic-images/direction2.png)
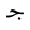
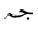
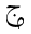
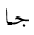

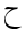
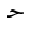
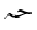
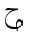
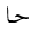

![[Image of literal summation]](arabic-images/mgmuec.png) and
and
![[Image of symbolic summation]](arabic-images/mgmues.png) ;
;![[Image of literal product]](arabic-images/gdaac.png) and
and
![[Image of symbolic product]](arabic-images/gdaas.png) ;
;![[Image of literal limit]](arabic-images/nhaytc.png) and
and
![[Image of limit in Persian style]](arabic-images/nhaytf.png) .
This last notation is used in Persian.
.
This last notation is used in Persian.![[Image of poorly stretched summation]](arabic-images/mgmuel.png)
![[Image of poorly stretched product]](arabic-images/gdaal.png)
![[Image of poorly stretched limit]](arabic-images/nhaytl.png)
![[Image of poorly stretched factorial]](arabic-images/drbl.png)
![[Image of stretched summation]](arabic-images/mgmuegl.png) and
and
![[Image of stretched product]](arabic-images/gdaagl.png) ,
this stretching is more common, and more desired, in Arabic mathematics:
,
this stretching is more common, and more desired, in Arabic mathematics:
![[Image of stretched mirrored summation]](arabic-images/mgmuega.png) and
and
![[Image of stretched mirrored product]](arabic-images/gdaaga.png) .
.