Additionally, each facet definition element can be uniquely
addressed via a URI constructed as follows:
Additionally, each facet usage in a built-in datatype definition
can be uniquely addressed via a URI constructed as follows:
For example, to address the usage of the maxInclusive facet in
the definition of int, the URI is:

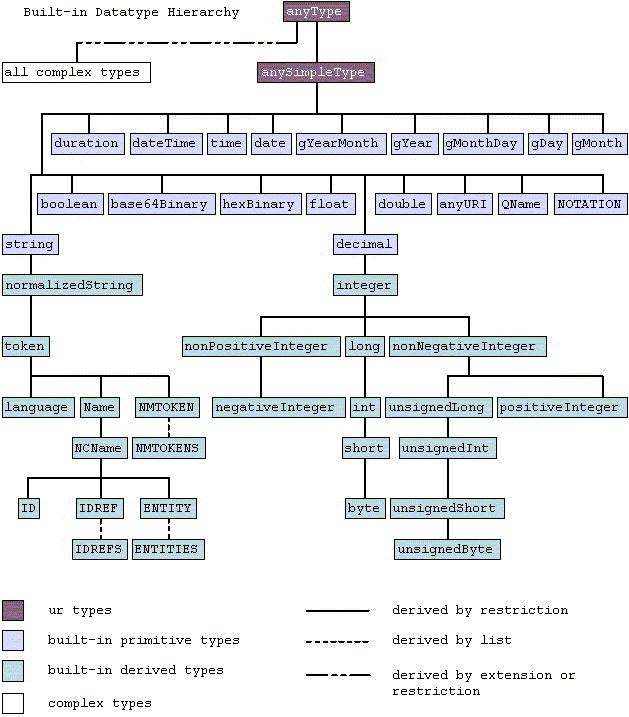
 3.2 Primitive datatypes
3.2 Primitive datatypes
The ·primitive· datatypes defined by this specification
are described below. For each datatype, the
·value space· and ·lexical space·
are defined, ·constraining facet·s which apply
to the datatype are listed and any datatypes ·derived·
from this datatype are specified.
·primitive· datatypes can only be added by revisions
to this specification.
3.2.1 string
[Definition:] The string datatype
represents character strings in XML. The ·value space·
of string is the set of finite-length sequences of
characters (as defined in
[XML]) that ·match· the
Char production from [XML].
A character is an atomic unit of
communication; it is not further specified except to note that every
character has a corresponding
Universal Character Set code point, which is an integer.
Note:
As noted in
ordered, the fact that this specification does
not specify an
·order-relation· for
·string·
does not preclude other applications from treating strings as being ordered.
3.2.2 boolean
[Definition:] boolean has the
·value space· required to support the mathematical
concept of binary-valued logic: {true, false}.
3.2.2.1 Lexical representation
An instance of a datatype that is defined as ·boolean·
can have the following legal literals {true, false, 1, 0}.
3.2.2.2 Canonical representation
The canonical representation for boolean is the set of
literals {true, false}.
3.2.3 decimal
Issue (RQ-150i):RQ-150 (minimum nbr of digits for decimal)The minimum will be lowered to 16 digits; a health warning
will be added to indicate that optimized implementations of derived
datatypes may exceed the limits of the base, but are not required
to.
[Definition:] decimal
represents a subset of the real numbers, which can be represented by decimal numerals.
The ·value space· of decimal
is the set of
numbers that can be obtained by multiplying an integer by a non-positive
power of ten, i.e., expressible as i × 10^-n
where i and n are integers
and n >= 0.
Precision is not reflected in this value space;
the number 2.0 is not distinct from the number 2.00.
The ·order-relation· on decimal
is the order relation on real numbers, restricted
to this subset.
Note:
All
·minimally conforming· processors
·must·
support decimal numbers with a minimum of 18 decimal digits (i.e., with a
·totalDigits· of 18). However,
·minimally conforming· processors
·may·
set an application-defined limit on the maximum number of decimal digits
they are prepared to support, in which case that application-defined
maximum number
·must· be clearly documented.
3.2.3.1 Lexical representation
decimal has a lexical representation
consisting of a finite-length sequence of decimal digits (#x30-#x39) separated
by a period as a decimal indicator.
An optional leading sign is allowed.
If the sign is omitted, "+" is assumed. Leading and trailing zeroes are optional.
If the fractional part is zero, the period and following zero(es) can
be omitted.
For example: -1.23, 12678967.543233, +100000.00, 210.
3.2.3.2 Canonical representation
The canonical representation for decimal is defined by
prohibiting certain options from the
Lexical representation (§3.2.3.1). Specifically, the preceding
optional "+" sign is prohibited. The decimal point is required. Leading and
trailing zeroes are prohibited subject to the following: there must be at least
one digit to the right and to the left of the decimal point which may be a zero.
3.2.4 float
[Definition:] float
is patterned after the IEEE single-precision 32-bit floating point type
[IEEE 754-1985]. The basic ·value space· of
float consists of the values
m × 2^e, where m
is an integer whose absolute value is less than
2^24, and e is an integer
between -149 and 104, inclusive. In addition to the basic
·value space· described above, the
·value space· of float also contains the
following
three
special values:
positive and negative infinity and not-a-number
(NaN).
The ·order-relation· on float
is: x < y iff y - x is positive
for x and y in the value space.
Positive infinity is greater than all other non-NaN values.
NaN equals itself but is incomparable with (neither greater than nor less than)
any other value in the ·value space·.
Note:
"Equality" in this Recommendation is defined to be "identity" (i.e., values that
are identical in the
·value space· are equal and vice versa).
Identity must be used for the few operations that are defined in this Recommendation.
Applications using any of the datatypes defined in this Recommendation may use different
definitions of equality for computational purposes;
[IEEE 754-1985]-based computation systems
are examples. Nothing in this Recommendation should be construed as requiring that
such applications use identity as their equality relationship when computing.
Any value incomparable with the value used for the four bounding facets
(
·minInclusive·,
·maxInclusive·,
·minExclusive·, and
·maxExclusive·) will be
excluded from the resulting restricted
·value space·. In particular,
when "NaN" is used as a facet value for a bounding facet, since no other
float values are
·comparable· with it, the result is a
·value space·
either having NaN as its only member (the inclusive cases) or that is empty
(the exclusive cases). If any other value is used for a bounding facet,
NaN will be excluded from the resulting restricted
·value space·;
to add NaN back in requires union with the NaN-only space.
This datatype differs from that of
[IEEE 754-1985] in that there is only one
NaN and only one zero. This makes the equality and ordering of values in the data
space differ from that of
[IEEE 754-1985] only in that for schema purposes NaN = NaN.
A literal in the ·lexical space· representing a
decimal number d maps to the normalized value
in the ·value space· of float that is
closest to d in the sense defined by
[Clinger, WD (1990)]; if d is
exactly halfway between two such values then the even value is chosen.
3.2.4.1 Lexical representation
float values have a lexical representation
consisting of a mantissa followed, optionally, by the character
"E" or "e", followed by an exponent. The exponent ·must·
be an integer. The mantissa must be a decimal number. The representations
for exponent and mantissa must follow the lexical rules for
integer and decimal. If the "E" or "e" and
the following exponent are omitted, an exponent value of 0 is assumed.
The special values
positive
and negative infinity and not-a-number have lexical representations
INF, -INF and
NaN, respectively.
Lexical representations for zero may take a positive or negative sign.
For example, -1E4, 1267.43233E12, 12.78e-2, 12
, -0, 0
and INF are all legal literals for float.
3.2.4.2 Canonical representation
The canonical representation for float is defined by
prohibiting certain options from the
Lexical representation (§3.2.4.1). Specifically, the exponent
must be indicated by "E". Leading zeroes and the preceding optional "+" sign
are prohibited in the exponent.
If the exponent is zero, it must be indicated by "E0".
For the mantissa, the preceding optional "+" sign is prohibited
and the decimal point is required.
Leading and trailing zeroes are prohibited subject to the following:
number representations must
be normalized such that there is a single digit
which is non-zero
to the left of the decimal point and at least a single digit to the
right of the decimal point
unless the value being represented is zero. The canonical
representation for zero is 0.0E0.
3.2.5 double
[Definition:] The double
datatype
is patterned after the
IEEE double-precision 64-bit floating point
type [IEEE 754-1985]. The basic ·value space·
of double consists of the values
m × 2^e, where m
is an integer whose absolute value is less than
2^53, and e is an
integer between -1075 and 970, inclusive. In addition to the basic
·value space· described above, the
·value space· of double also contains
the following
three
special values:
positive and negative infinity and not-a-number
(NaN).
The ·order-relation· on double
is: x < y iff y - x is positive
for x and y in the value space.
Positive infinity is greater than all other non-NaN values.
NaN equals itself but is incomparable with (neither greater than nor less than)
any other value in the ·value space·.
Note:
"Equality" in this Recommendation is defined to be "identity" (i.e., values that
are identical in the
·value space· are equal and vice versa).
Identity must be used for the few operations that are defined in this Recommendation.
Applications using any of the datatypes defined in this Recommendation may use different
definitions of equality for computational purposes;
[IEEE 754-1985]-based computation systems
are examples. Nothing in this Recommendation should be construed as requiring that
such applications use identity as their equality relationship when computing.
Any value incomparable with the value used for the four bounding facets
(
·minInclusive·,
·maxInclusive·,
·minExclusive·, and
·maxExclusive·) will be
excluded from the resulting restricted
·value space·. In particular,
when "NaN" is used as a facet value for a bounding facet, since no other
double values are
·comparable· with it, the result is a
·value space·
either having NaN as its only member (the inclusive cases) or that is empty
(the exclusive cases). If any other value is used for a bounding facet,
NaN will be excluded from the resulting restricted
·value space·;
to add NaN back in requires union with the NaN-only space.
This datatype differs from that of
[IEEE 754-1985] in that there is only one
NaN and only one zero. This makes the equality and ordering of values in the data
space differ from that of
[IEEE 754-1985] only in that for schema purposes NaN = NaN.
A literal in the ·lexical space· representing a
decimal number d maps to the normalized value
in the ·value space· of double that is
closest to d; if d is
exactly halfway between two such values then the even value is chosen.
This is the best approximation of d
([Clinger, WD (1990)], [Gay, DM (1990)]), which is more
accurate than the mapping required by [IEEE 754-1985].
3.2.5.1 Lexical representation
double values have a lexical representation
consisting of a mantissa followed, optionally, by the character "E" or
"e", followed by an exponent. The exponent ·must· be
an integer. The mantissa must be a decimal number. The representations
for exponent and mantissa must follow the lexical rules for
integer and decimal. If the "E" or "e"
and the following exponent are omitted, an exponent value of 0 is assumed.
The special values
positive
and negative infinity and not-a-number have lexical representations
INF, -INF and
NaN, respectively.
Lexical representations for zero may take a positive or negative sign.
For example, -1E4, 1267.43233E12, 12.78e-2, 12
, -0, 0
and INF
are all legal literals for double.
3.2.5.2 Canonical representation
The canonical representation for double is defined by
prohibiting certain options from the
Lexical representation (§3.2.5.1). Specifically, the exponent
must be indicated by "E". Leading zeroes and the preceding optional "+" sign
are prohibited in the exponent.
If the exponent is zero, it must be indicated by "E0".
For the mantissa, the preceding optional "+" sign is prohibited
and the decimal point is required.
Leading and trailing zeroes are prohibited subject to the following:
number representations must
be normalized such that there is a single digit
which is non-zero
to the left of the decimal point and at least a single digit to the
right of the decimal point
unless the value being represented is zero. The canonical
representation for zero is 0.0E0.
3.2.6 precisionDecimal
Issue (RQ-31i):RQ-31 (precisionDecimal)precisionDecimal has been added. It is possible that precisionDecimal will replace decimal.
[Definition:] The precisionDecimal
datatype is similar to decimal, except that each value carries with
it a precision as well as a numeric value; it also includes special values for positive and
negative infinity and "not a number", and differentiates between "positive
zero" and "negative zero". "Precision"
is explained in Precision (§D.1.1). The special values are introduced to
make the datatype correspond closely to decimal datatypes whose definition
is planned for the next revision of IEEE/ANSI 754.
3.2.6.1 Value Space
a decimal number, positiveInfinity,
negativeInfinity or notANumber
Note: The
·sign· property is redundant except when
·numericalValue·
is zero; in other cases, the
·sign· value is fully determined by the
·numericalValue· value. Code optimization may well make it desirable
to separate out the
·sign· and the absolute value of the
·numericalValue·,
which will make implementation easier, but the verbal descriptions of such things as equality
and order somewhat more complicated.
Note: As explained below, the lexical
representation of the
precisionDecimal value object whose
·numericalValue·
is
notANumber is '
NaN'. Accordingly, in English text we
use 'NaN' to refer to that value. Similarly we use 'INF'
and '–INF' to refer to the two value objects whose
·numericalValue·
is
positiveInfinity and
negativeInfinity. These three value objects
are also informally called "not-a-number", "positive infinity",
and "negative infinity".
Equality and order for precisionDecimal are defined as follows:
- Two numerical precisionDecimal values
are ordered (or equal) as their
·numericalValue· values are ordered (or equal). (This means the two zeros with
a given ·arthmeticPrecision· but different ·sign· are equal;
negative zeros are not ordered less than positive zeros.)
- INF is equal only to itself, and is greater than
–INF and all numerical precisionDecimal values.
- –INF is equal only to itself, and is less than
INF and all numerical precisionDecimal values.
- NaN is incomparable with all values, including itself.
3.2.6.2 Lexical Mapping
Editorial Note: The notation constraining facet has not yet been written
up. Its effect will be to remove some portions of the lexical mapping.
precisionDecimal's lexical space is the set of all
no-decimal-point, decimal, and scientific numerals,
plus the character strings 'INF', '+INF', '-INF',
and 'NaN'. (Lexical representations of numbers
are traditionally called "numerals".) The notation
constraining facet can remove any one or two of the three subsets of
numerals, with corresponding reductions in the value space. Using this facet
rather than pattern will change the canonical
mapping to insure that the resulting datatype will still have canonical
representations of all its values.
Note: Canonical mappings are not used during schema processing. They are provided in this specification for
the benefit of other users of these datatype definitions who may find them useful, and for other specifications
which might find it useful to reference them normatively.
3.2.6.3 Constraining Facets
Editorial Note: The notation constraining facet has not yet been written
up. It's effect will be to remove some portions of the lexical mapping.
precisionDecimal has the following ·constraining facets·:
- fractionDigits
- minFractionDigits
- totalDigits
- specials
- notation constraining
- maxInclusive
- maxExclusive
- minInclusive
- minExclusive
- pattern
- whitespace
- eunmeration
3.2.7 duration
[Definition:] duration
is a datatype that represents
durations of time. The concept of duration being
captured is drawn from those of [ISO 8601], specifically durations
without fixed endpoints. For
example, "15 days" (whose most common lexical representation
in duration is 'P15D') is a duration value; "15 days
beginning 12 July 1995" and "15 days ending 12 July 1995" are not.
duration can provide addition and subtraction operations between duration values
and between duration/dateTime value pairs, and can be the result of subtracting
dateTime values. However, only addition to and subtraction from dateTime
is required for XML Schema processing and is defined in Adding durations to dateTimes (§H)
3.2.7.1 Value Space
Durations can be modeled in at least two ways: as six-property tuples (similar to
the seven-property model used for other date/time datatypes) or as two-property tuples
(somewhat similar to the alternative one-property timeOnTimeline model especially useful for
dateTime order). For
durations, it is useful to use the latter: duration values are two-property
tuples. (Note, however, that the
six-property model was implicitly used in Schema 1.0. The only effective difference to the user caused
by this change is in the canonical representations.) See
The Seven-property Model (§D.2.2) for more information on the seven-property model.
duration is partially ordered. Equality and order are defined in terms of that of
dateTime, and are determined by adding each duration value pair
in turn to the following four dateTime values:
- 1696-09-01T00:00:00Z
- 1697-02-01T00:00:00Z
- 1903-03-01T00:00:00Z
- 1903-07-01T00:00:00Z
If all four resulting dateTime value pairs are
ordered the same way (less than, equal, or greater than), then the
original pair of duration values is ordered the same way; otherwise the original pair
is incomparable.
Note: These four values are chosen so as to maximize
the possible differences in results that could occur, such as the difference when adding
P1M and P30D: 1697-02-01T00:00:00Z + P1M < 1697-02-01T00:00:00Z + P30D ,
but 1903-03-01T00:00:00Z + P1M > 1903-03-01T00:00:00Z + P30D , so
that P1M <> P30D . If two
duration values are ordered the same way
when added to each of these four
dateTime values, they will retain the same order when added
to
any other
dateTime values, unless one is within a leap-second and either the other
is also or is the beginning moment of the next second—in which case, the two results will
be equal even though the original
dateTime values were not. Therefore, two
duration values are
incomparable if and only if they can
ever result in different orders when added to
any
dateTime value not within a leap-second.
This minor anomaly is the result of having
duration unaware of leap-seconds while the
other date/time primitive datatypes are leap-second aware.
It turns out that under the definition just given, two duration
values are equal if and only if they are identical.
Note: There are many ways to implement
duration, some of which do not base the implementation
on the two-component model. This specification does not prescribe any particular implementation, as long as
the visible results are isomorphic to those described herein.
3.2.7.2 Lexical Space
The ·lexical representations· of duration are
more or less based on the pattern:
PnYnMnDTnHnMnS
More precisely, the ·lexical space· of duration is the set of character
strings that satisfy durationLexicalRep as defined by the following productions:
Lexical Representation Fragments
Thus, a durationLexicalRep consists of one or more of a duYearFrag,
duMonthFrag, duDayFrag, duHourFrag,
duMinuteFrag, and/or duSecondFrag, in order, with letters
'P' and 'T' (and perhaps a '-') where appropriate.
The durationLexicalRep production is equivalent to this regular expression
-?P(((([0-9]+Y([0-9]+M)?)|
( ([0-9]+M) ) )(([0-9]+D(T(([0-9]+H([0-9]+M)?([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+M) ([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+(\.[0-9]+)?S) ) ))?)|
( (T(([0-9]+H([0-9]+M)?([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+M) ([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+(\.[0-9]+)?S) ) )) ) )?)|
( (([0-9]+D(T(([0-9]+H([0-9]+M)?([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+M) ([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+(\.[0-9]+)?S) ) ))?)|
( (T(([0-9]+H([0-9]+M)?([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+M) ([0-9]+(\.[0-9]+)?S)?)|
( ([0-9]+(\.[0-9]+)?S) ) )) ) ) ) )
once you delete the
whitespace. Redundant parehtheses are shown as
"ghosts"; some find them helpful in reading the expression.)
The ·lexical mapping· for duration is called
"·durationMap·" herein.
Note: Canonical mappings are not used during schema processing. They are provided in this specification
for the benefit of other users of these datatype definitions who may find them useful, and for other specifications
which might find it useful to reference them normatively.
·The canonical mapping· for
duration is
called "·durationCanonicalMap·" herein.
3.2.8 dateTime
[Definition:]
dateTime values may be viewed as objects with integer-valued
year, month, day, hour and minute properties, a decimal-valued second property,
and a boolean timezoned property.
Each such object also has one decimal-valued
method or computed property, timeOnTimeline, whose value is always a decimal
number; the values are dimensioned in seconds, the integer 0 is
0001-01-01T00:00:00 and the value of timeOnTimeline for other dateTime
values is computed using the Gregorian algorithm as modified for leap-seconds.
The timeOnTimeline values form two related "timelines", one for timezoned
values and one for non-timezoned values.
Each timeline is a copy of the ·value space· of decimal,
with integers given units of seconds.
The ·value space· of
dateTime is closely related to the dates and times described in ISO 8601.
For clarity, the text above specifies a particular origin point for the
timeline.
It should be noted, however, that schema processors need not expose the
timeOnTimeline value to schema users, and there is no requirement that a
timeline-based implementation use the particular origin described here in
its internal representation.
Other interpretations of the ·value space· which lead to the
same results (i.e., are isomorphic) are of course acceptable.
All timezoned times are Coordinated Universal Time (·UTC·, sometimes called
"Greenwich Mean Time"). Other timezones indicated in lexical representations
are converted to ·UTC· during conversion of literals to values.
"Local" or untimezoned times are presumed to be the time in the timezone of some
unspecified locality as prescribed by the appropriate legal authority;
currently there are no legally prescribed timezones which are durations
whose magnitude is greater than 14 hours. The value of each numeric-valued property
(other than timeOnTimeline) is limited to the maximum value within the interval
determined by the next-higher property. For example, the day value can never be 32,
and cannot even be 29 for month 02 and year 2002 (February 2002).
Note:
The date and time datatypes described in this recommendation were inspired
by
[ISO 8601]. '0001' is the lexical representation of the year 1 of the Common Era
(1
CE, sometimes written "AD 1" or "1 AD"). There is no year 0, and '0000' is not a valid lexical representation. '-0001' is the lexical representation of the year 1 Before
Common Era (1 BCE, sometimes written "1 BC").
Those using this (1.0) version of this Recommendation to
represent negative years should be aware that the interpretation of lexical
representations beginning with a
'-' is likely to change in
subsequent versions.
[ISO 8601]
makes no mention of the year 0; in
[ISO 8601:1998 Draft Revision]
the form '0000' was disallowed and this recommendation disallows it as well.
However,
[ISO 8601:2000 Second Edition], which became available just as we were completing version
1.0, allows the form '0000', representing the year 1 BCE. A number of external commentators
have also suggested that '0000' be
allowed, as the lexical representation for 1 BCE, which is the normal usage in
astronomical contexts.
It is the intention of the XML Schema
Working Group to allow '0000' as a lexical representation in the
dateTime,
date,
gYear, and
gYearMonth datatypes in a subsequent version
of this Recommendation. '0000' will be the lexical representation of 1
BCE (which is a leap year), '-0001' will become the lexical representation of 2
BCE (not 1 BCE as in this (1.0) version), '-0002' of 3 BCE, etc.
Note: See the conformance note in
(§C) which
applies to this datatype as well.
3.2.8.1 Lexical representation
The ·lexical space· of dateTime consists of
finite-length sequences of characters of the form:
'-'? yyyy '-' mm '-' dd 'T' hh ':' mm ':' ss ('.' s+)? (zzzzzz)?,
where
- '-'? yyyy is a four-or-more digit optionally negative-signed
numeral that represents the year; if more than four digits, leading zeros
are prohibited, and '0000' is prohibited (see the Note above (§3.2.8); also note that a plus sign is not permitted);
- the remaining '-'s are separators between parts of the date portion;
- the first mm is a two-digit numeral that represents the month;
- dd is a two-digit numeral that represents the day;
- 'T' is a separator indicating that time-of-day follows;
- hh is a two-digit numeral that represents the hour; '24' is permitted if the
minutes and seconds represented are zero, and the dateTime value so
represented is the first instant of the following day (the hour property of a
dateTime object in the ·value space· cannot have
a value greater than 23);
- ':' is a separator between parts of the time-of-day portion;
- the second mm is a two-digit numeral that represents the minute;
- ss is a two-integer-digit numeral that represents the
whole seconds;
- '.' s+ (if present) represents the
fractional seconds;
- zzzzzz (if present) represents the timezone (as described below).
For example, 2002-10-10T12:00:00-05:00 (noon on 10 October 2002, Central Daylight
Savings Time as well as Eastern Standard Time in the U.S.) is 2002-10-10T17:00:00Z,
five hours later than 2002-10-10T12:00:00Z.
For further guidance on arithmetic with dateTimes and durations,
see Adding durations to dateTimes (§H).
3.2.8.2 Canonical representation
Except for trailing fractional zero digits in the seconds representation,
'24:00:00' time representations, and timezone (for timezoned values), the mapping
from literals to values is one-to-one. Where there is more than
one possible representation, the canonical representation is as follows:
- The 2-digit numeral representing the hour must not be '
24'; - The fractional second string, if present, must not end in '
0'; - for timezoned values, the timezone must be
represented with '
Z'
(All timezoned dateTime values are ·UTC·.).
3.2.8.3 Timezones
Timezones are durations with (integer-valued) hour and minute properties
(with the hour magnitude limited to at most 14, and the minute magnitude
limited to at most 59, except that if the hour magnitude is 14, the minute
value must be 0); they may be both positive or both negative.
The lexical representation of a timezone is a string of the form:
(('+' | '-') hh ':' mm) | 'Z',
where
- hh is a two-digit numeral (with leading zeros as required) that
represents the hours,
- mm is a two-digit numeral that represents the minutes,
- '+' indicates a nonnegative duration,
- '-' indicates a nonpositive duration.
The mapping so defined is one-to-one, except that '+00:00', '-00:00', and 'Z'
all represent the same zero-length duration timezone, ·UTC·; 'Z' is its canonical
representation.
When a timezone is added to a ·UTC· dateTime, the result is the date
and time "in that timezone". For example, 2002-10-10T12:00:00+05:00 is
2002-10-10T07:00:00Z and 2002-10-10T00:00:00+05:00 is 2002-10-09T19:00:00Z.
3.2.8.4 Order relation on dateTime
dateTime value objects on either timeline are totally ordered by their timeOnTimeline
values; between the two timelines, dateTime value objects are ordered by their
timeOnTimeline values when their timeOnTimeline values differ by more than
fourteen hours, with those whose difference is a duration of 14 hours or less
being incomparable.
In general, the ·order-relation· on dateTime
is a partial order since there is no determinate relationship between certain
instants. For example, there is no determinate
ordering between
(a)
2000-01-20T12:00:00 and (b) 2000-01-20T12:00:00Z. Based on
timezones currently in use, (c) could vary from 2000-01-20T12:00:00+12:00 to
2000-01-20T12:00:00-13:00. It is, however, possible for this range to expand or
contract in the future, based on local laws. Because of this, the following
definition uses a somewhat broader range of indeterminate values: +14:00..-14:00.
The following definition uses the notation S[year] to represent the year
field of S, S[month] to represent the month field, and so on. The notation (Q
& "-14:00") means adding the timezone -14:00 to Q, where Q did not
already have a timezone. This is a logical explanation of the process. Actual
implementations are free to optimize as long as they produce the same results.
The ordering between two dateTimes P and Q is defined by the following
algorithm:
A.Normalize P and Q. That is, if there is a timezone present, but
it is not Z, convert it to Z using the addition operation defined in
Adding durations to dateTimes (§H)
- Thus 2000-03-04T23:00:00+03:00 normalizes to 2000-03-04T20:00:00Z
B. If P and Q either both have a time zone or both do not have a time
zone, compare P and Q field by field from the year field down to the
second field, and return a result as soon as it can be determined. That is:
- For each i in {year, month, day, hour, minute, second}
- If P[i] and Q[i] are both not specified, continue to the next i
- If P[i] is not specified and Q[i] is, or vice versa, stop and return
P <> Q
- If P[i] < Q[i], stop and return P < Q
- If P[i] > Q[i], stop and return P > Q
- Stop and return P = Q
C.Otherwise, if P contains a time zone and Q does not, compare
as follows:
- P < Q if P < (Q with time zone +14:00)
- P > Q if P > (Q with time zone -14:00)
- P <> Q otherwise, that is, if (Q with time zone +14:00) < P < (Q with time zone -14:00)
D. Otherwise, if P does not contain a time zone and Q does, compare
as follows:
- P < Q if (P with time zone -14:00) < Q.
- P > Q if (P with time zone +14:00) > Q.
- P <> Q otherwise, that is, if (P with time zone +14:00) < Q < (P with time zone -14:00)
Examples:
| Determinate | Indeterminate |
|---|
| 2000-01-15T00:00:00 < 2000-02-15T00:00:00 | 2000-01-01T12:00:00 <>
1999-12-31T23:00:00Z |
| 2000-01-15T12:00:00 < 2000-01-16T12:00:00Z | 2000-01-16T12:00:00 <>
2000-01-16T12:00:00Z |
| | 2000-01-16T00:00:00 <> 2000-01-16T12:00:00Z |
3.2.8.5 Totally ordered dateTimes
Certain derived types from dateTime
can be guaranteed have a total order. To
do so, they must require that a specific set of fields are always specified, and
that remaining fields (if any) are always unspecified. For example, the date
datatype without time zone is defined to contain exactly year, month, and day.
Thus dates without time zone have a total order among themselves.
3.2.9 time
[Definition:] time
represents an instant of time that recurs every day. The
·value space· of time is the space
of time of day values as defined in § 5.3 of
[ISO 8601]. Specifically, it is a set of zero-duration daily
time instances.
Since the lexical representation allows an optional time zone
indicator, time values are partially ordered because it may
not be able to determine the order of two values one of which has a
time zone and the other does not. The order relation on
time values is the
Order relation on dateTime (§3.2.8.4) using an arbitrary date. See also
Adding durations to dateTimes (§H). Pairs of time values with or without time zone indicators are totally ordered.
Note: See the conformance note in
(§C) which
applies to the seconds part of this datatype as well.
3.2.9.1 Lexical representation
The lexical representation for time is the left
truncated lexical representation for dateTime:
hh:mm:ss.sss with optional following time zone indicator. For example,
to indicate 1:20 pm for Eastern Standard Time which is 5 hours behind
Coordinated Universal Time (·UTC·), one would write: 13:20:00-05:00. See also
ISO 8601 Date and Time Formats (§G).
3.2.9.2 Canonical representation
The canonical representation for time is defined
by prohibiting certain options from the
Lexical representation (§3.2.9.1). Specifically, either the time zone must
be omitted or, if present, the time zone must be Coordinated Universal
Time (·UTC·) indicated by a "Z".
Additionally, the canonical representation for midnight is 00:00:00.
3.2.10 date
[Definition:]
The ·value space· of date
consists of top-open intervals of exactly one day in length on the timelines of
dateTime, beginning on the beginning moment of each day (in
each timezone), i.e. '00:00:00', up to but not including '24:00:00' (which is
identical with '00:00:00' of the next day). For nontimezoned values, the top-open
intervals disjointly cover the nontimezoned timeline, one per day. For timezoned
values, the intervals begin at every minute and therefore overlap.
A "date object" is an object with year, month, and day properties just like those
of dateTime objects, plus an optional timezone-valued
timezone property. (As with values of dateTime timezones are a
special case of durations.)
Just as a dateTime object corresponds to a point on one of the
timelines, a date object corresponds to an interval on one
of the two timelines as just described.
Timezoned date values track the starting moment of their day, as
determined by their timezone; said timezone is generally recoverable for
canonical representations.
[Definition:]
The recoverable timezone is that duration which
is the result of subtracting the first moment (or any moment) of the timezoned
date from the first moment (or the corresponding moment) ·UTC· on the
same date. ·recoverable timezone·s are
always durations between '+12:00' and '-11:59'. This "timezone normalization"
(which follows automatically from the definition of the date
·value space·) is explained more in
Lexical representation (§3.2.10.1).
For example: the first moment of 2002-10-10+13:00 is 2002-10-10T00:00:00+13,
which is 2002-10-09T11:00:00Z, which is also the first moment of 2002-10-09-11:00.
Therefore 2002-10-10+13:00 is 2002-10-09-11:00; they are the same interval.
Note:
For most timezones, either the first moment or last moment of the day (a
dateTime value, always
·UTC·) will have a
date portion
different from that of the
date itself!
However, noon of that
date (the midpoint of the interval) in that
(normalized) timezone will always have the same
date portion as the
date itself, even when that noon point in time is normalized to
·UTC·. For example, 2002-10-10-05:00 begins during 2002-10-09Z and 2002-10-10+05:00
ends during 2002-10-11Z, but noon of both 2002-10-10-05:00 and 2002-10-10+05:00
falls in the interval which is 2002-10-10Z.
Note: See the conformance note in
(§C) which
applies to the year part of this datatype as well.
3.2.10.1 Lexical representation
For the following discussion, let the "date portion" of a dateTime
or date object be an object similar to a dateTime or
date object, with similar year, month, and day properties, but no
others, having the same value for these properties as the original
dateTime or date object.
The ·lexical space· of date consists of finite-length
sequences of characters of the form:
'-'? yyyy '-' mm '-' dd zzzzzz?
where the date and optional timezone are represented exactly the
same way as they are for dateTime. The first moment of the
interval is that represented by:
'-' yyyy '-' mm '-' dd 'T00:00:00' zzzzzz?
and the least upper bound of the interval is the timeline point represented
(noncanonically) by:
'-' yyyy '-' mm '-' dd 'T24:00:00' zzzzzz?.
Note:
The
·recoverable timezone· of a
date will always be
a duration between '+12:00' and '11:59'. Timezone lexical representations, as
explained for
dateTime, can range from '+14:00' to '-14:00'.
The result is that literals of
dates with very large or very
negative timezones will map to a "normalized"
date value with a
·recoverable timezone· different from that represented in the original
representation, and a matching difference of +/- 1 day in the
date itself.
3.2.10.2 Canonical representation
Given a member of the date ·value space·, the
date portion of the canonical representation (the entire representation
for nontimezoned values, and all but the timezone representation for timezoned values)
is always the date portion of the dateTime canonical
representation of the interval midpoint (the dateTime representation,
truncated on the right to eliminate 'T' and all following characters).
For timezoned values, append the canonical representation of the ·recoverable timezone·.
3.2.11 gYearMonth
[Definition:]
gYearMonth represents a
specific gregorian month in a specific gregorian year. The
·value space· of gYearMonth
is the set of Gregorian calendar months as defined in § 5.2.1 of
[ISO 8601]. Specifically, it is a set of one-month long,
non-periodic instances
e.g. 1999-10 to represent the whole month of 1999-10, independent of
how many days this month has.
Since the lexical representation allows an optional time zone
indicator, gYearMonth values are partially ordered because it may
not be possible to unequivocally determine the order of two values one of
which has a time zone and the other does not. If gYearMonth
values are considered as periods of time, the order relation on
gYearMonth values is the order relation on their starting instants.
This is discussed in Order relation on dateTime (§3.2.8.4). See also
Adding durations to dateTimes (§H). Pairs of gYearMonth
values with or without time zone indicators are totally ordered.
Note:
Because month/year combinations in one calendar only rarely correspond
to month/year combinations in other calendars, values of this type
are not, in general, convertible to simple values corresponding to month/year
combinations in other calendars. This type should therefore be used with caution
in contexts where conversion to other calendars is desired.
Note: See the conformance note in
(§C) which
applies to the year part of this datatype as well.
3.2.11.1 Lexical representation
The lexical representation for gYearMonth is the reduced
(right truncated) lexical representation for dateTime:
CCYY-MM. No left truncation is allowed. An optional following time
zone qualifier is allowed. To accommodate year values outside the range from 0001 to 9999, additional digits
can be added to the left of this representation and a preceding "-" sign is allowed.
For example, to indicate the month of May 1999, one would write: 1999-05.
See also ISO 8601 Date and Time Formats (§G).
3.2.12 gYear
[Definition:]
gYear represents a
gregorian calendar year. The ·value space· of
gYear is the set of Gregorian calendar years as defined in
§ 5.2.1 of [ISO 8601]. Specifically, it is a set of one-year
long, non-periodic instances
e.g. lexical 1999 to represent the whole year 1999, independent of
how many months and days this year has.
Since the lexical representation allows an optional time zone
indicator, gYear values are partially ordered because it may
not be possible to unequivocally determine the order of two values one of which has a
time zone and the other does not. If
gYear values are considered as periods of time, the order relation
on gYear values is the order relation on their starting instants.
This is discussed in Order relation on dateTime (§3.2.8.4). See also
Adding durations to dateTimes (§H). Pairs of gYear values with or without time zone indicators are totally ordered.
Note:
Because years in one calendar only rarely correspond to years
in other calendars, values of this type
are not, in general, convertible to simple values corresponding to years
in other calendars. This type should therefore be used with caution
in contexts where conversion to other calendars is desired.
Note: See the conformance note in
(§C) which
applies to the year part of this datatype as well.
3.2.12.1 Lexical representation
The lexical representation for gYear is the reduced (right
truncated) lexical representation for dateTime: CCYY.
No left truncation is allowed. An optional following time
zone qualifier is allowed as for dateTime. To
accommodate year values outside the range from 0001 to 9999, additional
digits can be added to the left of this representation and a preceding
"-" sign is allowed.
For example, to indicate 1999, one would write: 1999.
See also ISO 8601 Date and Time Formats (§G).
3.2.13 gMonthDay
[Definition:]
gMonthDay is a gregorian date that recurs, specifically a day of
the year such as the third of May. Arbitrary recurring dates are not
supported by this datatype. The ·value space· of
gMonthDay is the set of calendar
dates, as defined in § 3 of [ISO 8601]. Specifically,
it is a set of one-day long, annually periodic instances.
Since the lexical representation allows an optional time zone
indicator, gMonthDay values are partially ordered because it may
not be possible to unequivocally determine the order of two values one of which has a
time zone and the other does not. If
gMonthDay values are considered as periods of time,
in an arbitrary leap year, the order relation
on gMonthDay values is the order relation on their starting instants.
This is discussed in Order relation on dateTime (§3.2.8.4). See also
Adding durations to dateTimes (§H). Pairs of gMonthDay values with or without time zone indicators are totally ordered.
Note:
Because day/month combinations in one calendar only rarely correspond
to day/month combinations in other calendars, values of this type do not,
in general, have any straightforward or intuitive representation
in terms of most other calendars. This type should therefore be
used with caution in contexts where conversion to other calendars
is desired.
3.2.13.1 Lexical representation
The lexical representation for gMonthDay is the left
truncated lexical representation for date: --MM-DD.
An optional following time
zone qualifier is allowed as for date.
No preceding sign is allowed. No other formats are allowed. See also ISO 8601 Date and Time Formats (§G).
This datatype can be used to represent a specific day in a month.
To say, for example, that my birthday occurs on the 14th of September ever year.
3.2.14 gDay
[Definition:] gDay is a datatype
that represents whole days within an arbitrary month—days that recur at the same
point in each (Gregorian) month. This datatype is used to represent a specific day of the month.
To indicate, for example, that an employee gets a paycheck on the 15th of each month. (Obviously, days
beyond 28 cannot occur in all months; they are nonetheless permitted, up to 31.)
Note:
Because days in one calendar only rarely correspond
to days in other calendars, gday values do not,
in general, have any straightforward or intuitive representation
in terms of most non-Gregorian calendars. gday should therefore be
used with caution in contexts where conversion to other calendars
is desired.
3.2.14.1 Value Space
gDay uses the date/timeSevenPropertyModel, with
·year·, ·month·, ·hour·, ·minute·,
and ·second· required to be absent. ·timezone· remains
·optional· and ·day· must be between 1 and 31 inclusive.
Issue (RQ-13i):RQ-13 (time zone crosses date line)The "seven property model" rewrite of date/time datatype descriptions includes a carefully crafted definition of order
that insures that for repeating datatypes (time, gDay, etc.), timezoned values will be compared as though they are on the same "calendar day" ("raw"
property values) so that in any given timezone, the days start at "raw" 00:00:00 and end not quite including "raw" 24:00:00. Days are not
00:00:00Z to 24:00:00Z in timezones other than Z.
Equality and order are as prescribed in The Seven-property Model (§D.2.2). Since gDay
values (days) are ordered by their first moments, it is possible
for apparent anomalies to appear in the order when ·timezone· values are differ by at least 24
hours. (It is possible for ·timezone· values to differ by up to 28 hours.)
Examples that may appear anomalous (see Lexical Mappings (§3.2.14.3) for the notations):
- ---15 < ---16 , but ---15–13:00 > ---16+13:00
- ---15–11:00 = ---16+13:00
- ---15–13:00 <> ---16 ,
because ---15–13:00 > ---16+14:00
and ---15–13:00 < 16–14:00
Note: Timezones do not cause wrap-around at the end of the month: ---31–13:00 in
one month may start after ---01+13:00 in the next month, but nonetheless
---01+13:00 < ---31–13:00 .
3.2.14.3 Lexical Mappings
The lexical representations for gDay are "restrictions" of
those of dateTime, as follows:
The gDayLexicalRep is equivalent to this regular expression:
---([0-2][0-9]|3[01])((+|-)(0[0-9]|1[0-4]):[0-5][0-9])?
The lexical mapping and canonical mapping for gDay are defined as follows:
3.2.15 gMonth
[Definition:]
gMonth is a gregorian month that recurs every year.
The ·value space·
of gMonth is the space of a set of calendar
months as defined in § 3 of [ISO 8601]. Specifically,
it is a set of one-month long, yearly periodic instances.
This datatype can be used to represent a specific month.
To say, for example, that Thanksgiving falls in the month of November.
Since the lexical representation allows an optional time zone
indicator, gMonth values are partially ordered because it may
not be possible to unequivocally determine the order of two values one of which has a
time zone and the other does not. If
gMonth values are considered as periods of time, the order relation
on gMonth is the order relation on their starting instants.
This is discussed in Order relation on dateTime (§3.2.8.4). See also
Adding durations to dateTimes (§H). Pairs of gMonth
values with or without time zone indicators are totally ordered.
Note:
Because months in one calendar only rarely correspond
to months in other calendars, values of this type do not,
in general, have any straightforward or intuitive representation
in terms of most other calendars. This type should therefore be
used with caution in contexts where conversion to other calendars
is desired.
3.2.15.1 Lexical representation
The lexical representation for gMonth is the left
and right truncated lexical representation for date: --MM.
An optional following time
zone qualifier is allowed as for date. No preceding sign is
allowed. No other formats are allowed. See also ISO 8601 Date and Time Formats (§G).
3.2.16 hexBinary
[Definition:]
hexBinary represents
arbitrary hex-encoded binary data. The ·value space· of
hexBinary is the set of finite-length sequences of binary
octets.
3.2.16.1 Lexical Representation
hexBinary has a lexical representation where
each binary octet is encoded as a character tuple, consisting of two
hexadecimal digits ([0-9a-fA-F]) representing the octet code. For example,
"0FB7" is a hex encoding for the 16-bit integer 4023
(whose binary representation is 111110110111).
3.2.16.2 Canonical Representation
The canonical representation for hexBinary is defined
by prohibiting certain options from the
Lexical Representation (§3.2.16.1). Specifically, the lower case
hexadecimal digits ([a-f]) are not allowed.
3.2.17 base64Binary
[Definition:]
base64Binary
represents Base64-encoded arbitrary binary data. The ·value space· of
base64Binary is the set of finite-length sequences of binary
octets. For base64Binary data the
entire binary stream is encoded using the Base64
Alphabet in
[RFC 2045].
The lexical forms of base64Binary values are limited to the 65 characters
of the Base64 Alphabet defined in [RFC 2045], i.e., a-z,
A-Z, 0-9, the plus sign (+), the forward slash (/) and the
equal sign (=), together with the characters defined in [XML] as white space.
No other characters are allowed.
For compatibility with older mail gateways, [RFC 2045] suggests that
base64 data should have lines limited to at most 76 characters in length. This
line-length limitation is not mandated in the lexical forms of base64Binary
data and must not be enforced by XML Schema processors.
The lexical space of base64Binary is given by the following grammar
(the notation is that used in [XML]); legal lexical forms must match
the Base64Binary production.
Base64Binary ::= ((B64S B64S B64S B64S)*
((B64S B64S B64S B64) |
(B64S B64S B16S '=') |
(B64S B04S '=' #x20? '=')))?
B64S ::= B64 #x20?
B16S ::= B16 #x20?
B04S ::= B04 #x20?
B04 ::= [AQgw]
B16 ::= [AEIMQUYcgkosw048]
B64 ::= [A-Za-z0-9+/]
Note that this grammar requires the number of non-whitespace characters in the lexical
form to be a multiple of four, and for equals signs to appear only at the end of the
lexical form; strings which do not meet these constraints are not legal lexical forms
of base64Binary because they cannot successfully be decoded by base64
decoders.
Note: The above definition of the lexical space is more restrictive than that
given in
[RFC 2045] as regards whitespace -- this is not an issue
in practice. Any string compatible with the RFC can occur in
an element or attribute validated by this type, because the
·whiteSpace· facet of this type is fixed
to
collapse, which means that all leading and trailing whitespace
will be stripped, and all internal whitespace collapsed to single space
characters,
before the above grammar is enforced.
The canonical lexical form of a base64Binary data value is the base64
encoding of the value which matches the Canonical-base64Binary production in the following
grammar:
Canonical-base64Binary ::= (B64
B64 B64 B64)*
((B64 B64 B16 '=') | (B64 B04 '=='))?
Note: For some values the canonical form defined above does not conform to
[RFC 2045], which requires
breaking with linefeeds at appropriate intervals.
The length of a base64Binary value is the number of octets it contains.
This may be calculated from the lexical form by removing whitespace and padding characters
and performing the calculation shown in the pseudo-code below:
lex2 := killwhitespace(lexform) -- remove whitespace characters
lex3 := strip_equals(lex2) -- strip padding characters at end
length := floor (length(lex3) * 3 / 4) -- calculate length
Note on encoding: [RFC 2045] explicitly references US-ASCII encoding. However,
decoding of base64Binary data in an XML entity is to be performed on the
Unicode characters obtained after character encoding processing as specified by
[XML]
3.2.18 anyURI
[Definition:]
anyURI represents a Uniform Resource Identifier Reference
(URI). An anyURI value can be absolute or relative, and may
have an optional fragment identifier (i.e., it may be a URI Reference). This
type should be used to specify the intention that the value fulfills
the role of a URI as defined by [RFC 2396], as amended by
[RFC 2732].
The mapping from anyURI values to URIs is as
defined by the URI reference escaping procedure
defined in
Section 5.4 Locator Attribute
of [XML Linking Language] (see also Section 7
Character Encoding in URI References
of [Character Model]). This means
that a wide range of internationalized resource identifiers can be specified
when an anyURI is called for, and still be understood as
URIs per [RFC 2396], as amended by [RFC 2732],
where appropriate to identify resources.
Note:
Section 5.4
Locator Attribute
of
[XML Linking Language] requires that relative URI references be absolutized
as defined in
[XML Base] before use. This is an XLink-specific
requirement and is not appropriate for XML Schema, since neither the
·lexical space· nor the
·value space·
of the
anyURI type are restricted to absolute URIs. Accordingly
absolutization must not be performed by schema processors as part of schema
validation.
Note:
Each URI scheme imposes specialized syntax rules for URIs in
that scheme, including restrictions on the syntax of allowed
fragment
identifiers. Because it is
impractical for processors to check that a value is a
context-appropriate URI reference, this specification follows the
lead of
[RFC 2396] (as amended by
[RFC 2732])
in this matter: such rules and restrictions are not part of type validity
and are not checked by
·minimally conforming· processors.
Thus in practice the above definition imposes only very modest obligations
on
·minimally conforming· processors.
3.2.18.1 Lexical representation
The ·lexical space· of anyURI is
finite-length character sequences which, when the algorithm defined in
Section 5.4 of [XML Linking Language] is applied to them, result in strings
which are legal URIs according to [RFC 2396], as amended by
[RFC 2732].
Note:
Spaces are, in principle, allowed in the
·lexical space·
of
anyURI, however, their use is highly discouraged
(unless they are encoded by %20).
3.2.20 NOTATION
[Definition:]
NOTATION
represents the NOTATION attribute
type from [XML]. The ·value space·
of NOTATION is the set of QNames
of notations declared in the current schema.
The ·lexical space· of NOTATION is the set
of all names of notations
declared in the current schema (in the form of QNames).
Schema Component Constraint: enumeration facet value required for NOTATION
It is an
·error· for
NOTATION
to be used directly in a schema. Only datatypes that are
·derived· from
NOTATION by
specifying a value for
·enumeration· can be used
in a schema.
For compatibility (see Terminology (§1.5)) NOTATION
should be used only on attributes
and should only be used in schemas with no
target namespace.
 3.3 Derived datatypes
3.3 Derived datatypes
This section gives conceptual definitions for all
·built-in· ·derived· datatypes
defined by this specification. The XML representation used to define
·derived· datatypes (whether
·built-in· or ·user-derived·) is
given in section XML Representation of Simple Type Definition Schema Components (§4.1.2) and the complete
definitions of the ·built-in·
·derived· datatypes are provided in Appendix A
Schema for Datatype Definitions (normative) (§A).
3.3.1 normalizedString
[Definition:]
normalizedString
represents white space normalized strings.
The ·value space· of normalizedString is the
set of strings that do not
contain the carriage return (#xD), line feed (#xA) nor tab (#x9) characters.
The ·lexical space· of normalizedString is the
set of strings that do not
contain the carriage return (#xD),
line feed (#xA)
nor tab (#x9) characters.
The ·base type· of normalizedString is string.
3.3.1.2 Derived datatypes
The following ·built-in·
datatypes are ·derived· from
normalizedString:
3.3.2 token
[Definition:]
token
represents tokenized strings.
The ·value space· of token is the
set of strings that do not
contain the
carriage return (#xD),
line feed (#xA) nor tab (#x9) characters, that have no
leading or trailing spaces (#x20) and that have no internal sequences
of two or more spaces.
The ·lexical space· of token is the
set of strings that do not contain the
carriage return (#xD),
line feed (#xA) nor tab (#x9) characters, that have no
leading or trailing spaces (#x20) and that have no internal sequences
of two or more spaces.
The ·base type· of token is normalizedString.
3.3.13 integer
[Definition:]
integer is
·derived· from decimal by fixing the
value of ·fractionDigits· to be 0and
disallowing the trailing decimal point.
This results in the standard
mathematical concept of the integer numbers. The
·value space· of integer is the infinite
set {...,-2,-1,0,1,2,...}. The ·base type· of
integer is decimal.
3.3.13.1 Lexical representation
integer has a lexical representation consisting of a finite-length sequence
of decimal digits (#x30-#x39) with an optional leading sign. If the sign is omitted,
"+" is assumed. For example: -1, 0, 12678967543233, +100000.
3.3.13.2 Canonical representation
The canonical representation for integer is defined
by prohibiting certain options from the
Lexical representation (§3.3.13.1). Specifically, the preceding optional "+" sign is prohibited and leading zeroes are prohibited.
3.3.14 nonPositiveInteger
[Definition:]
nonPositiveInteger is ·derived· from
integer by setting the value of
·maxInclusive· to be 0. This results in the
standard mathematical concept of the non-positive integers.
The ·value space· of nonPositiveInteger
is the infinite set {...,-2,-1,0}. The ·base type·
of nonPositiveInteger is integer.
3.3.14.1 Lexical representation
nonPositiveInteger has a lexical representation consisting of
an optional preceding sign
followed by a finite-length sequence of decimal digits (#x30-#x39).
The sign may be "+" or may be omitted only for
lexical forms denoting zero; in all other lexical forms, the negative
sign ("-") must be present.
For example: -1, 0, -12678967543233, -100000.
3.3.14.2 Canonical representation
The canonical representation for nonPositiveInteger is defined
by prohibiting certain options from the
Lexical representation (§3.3.14.1).
In the canonical form for zero, the sign must be
omitted. Leading zeroes are prohibited.
3.3.14.4 Derived datatypes
The following ·built-in·
datatypes are ·derived· from
nonPositiveInteger:
3.3.15 negativeInteger
[Definition:]
negativeInteger is ·derived· from
nonPositiveInteger by setting the value of
·maxInclusive· to be -1. This results in the
standard mathematical concept of the negative integers. The
·value space· of negativeInteger
is the infinite set {...,-2,-1}. The ·base type·
of negativeInteger is nonPositiveInteger.
3.3.15.1 Lexical representation
negativeInteger has a lexical representation consisting of
a negative sign ("-") followed by a finite-length
sequence of decimal digits (#x30-#x39). For example: -1, -12678967543233, -100000.
3.3.15.2 Canonical representation
The canonical representation for negativeInteger is defined
by prohibiting certain options from the
Lexical representation (§3.3.15.1). Specifically, leading zeroes are prohibited.
3.3.16 long
[Definition:]
long is
·derived· from integer by setting the
value of ·maxInclusive· to be 9223372036854775807
and ·minInclusive· to be -9223372036854775808.
The ·base type· of long is
integer.
3.3.16.1 Lexical representation
long has a lexical representation consisting
of an optional sign followed by a finite-length
sequence of decimal digits (#x30-#x39). If the sign is omitted, "+" is assumed.
For example: -1, 0,
12678967543233, +100000.
3.3.16.2 Canonical representation
The canonical representation for long is defined
by prohibiting certain options from the
Lexical representation (§3.3.16.1). Specifically, the
the optional "+" sign is prohibited and leading zeroes are prohibited.
3.3.17 int
[Definition:]
int
is ·derived· from long by setting the
value of ·maxInclusive· to be 2147483647 and
·minInclusive· to be -2147483648. The
·base type· of int is long.
3.3.17.1 Lexical representation
int has a lexical representation consisting
of an optional sign followed by a finite-length
sequence of decimal digits (#x30-#x39). If the sign is omitted, "+" is assumed.
For example: -1, 0,
126789675, +100000.
3.3.17.2 Canonical representation
The canonical representation for int is defined
by prohibiting certain options from the
Lexical representation (§3.3.17.1). Specifically, the
the optional "+" sign is prohibited and leading zeroes are prohibited.
3.3.18 short
[Definition:]
short is
·derived· from int by setting the
value of ·maxInclusive· to be 32767 and
·minInclusive· to be -32768. The
·base type· of short is
int.
3.3.18.1 Lexical representation
short has a lexical representation consisting
of an optional sign followed by a finite-length sequence of decimal
digits (#x30-#x39). If the sign is omitted, "+" is assumed.
For example: -1, 0, 12678, +10000.
3.3.18.2 Canonical representation
The canonical representation for short is defined
by prohibiting certain options from the
Lexical representation (§3.3.18.1). Specifically, the
the optional "+" sign is prohibited and leading zeroes are prohibited.
3.3.19 byte
[Definition:]
byte
is ·derived· from short
by setting the value of ·maxInclusive· to be 127
and ·minInclusive· to be -128.
The ·base type· of byte is
short.
3.3.19.1 Lexical representation
byte has a lexical representation consisting
of an optional sign followed by a finite-length
sequence of decimal digits (#x30-#x39). If the sign is omitted, "+" is assumed.
For example: -1, 0,
126, +100.
3.3.19.2 Canonical representation
The canonical representation for byte is defined
by prohibiting certain options from the
Lexical representation (§3.3.19.1). Specifically, the
the optional "+" sign is prohibited and leading zeroes are prohibited.
3.3.20 nonNegativeInteger
[Definition:]
nonNegativeInteger is ·derived· from
integer by setting the value of
·minInclusive· to be 0. This results in the
standard mathematical concept of the non-negative integers. The
·value space· of nonNegativeInteger
is the infinite set {0,1,2,...}. The ·base type· of
nonNegativeInteger is integer.
3.3.20.1 Lexical representation
nonNegativeInteger has a lexical representation consisting of
an optional sign followed by a finite-length
sequence of decimal digits (#x30-#x39). If the sign is omitted,
the positive sign ("+") is assumed.
If the sign is present, it must be "+" except for lexical forms
denoting zero, which may be preceded by a positive ("+") or a negative ("-") sign.
For example:
1, 0, 12678967543233, +100000.
3.3.20.2 Canonical representation
The canonical representation for nonNegativeInteger is defined
by prohibiting certain options from the
Lexical representation (§3.3.20.1). Specifically, the
the optional "+" sign is prohibited and leading zeroes are prohibited.
3.3.20.4 Derived datatypes
The following ·built-in·
datatypes are ·derived· from
nonNegativeInteger:
3.3.21 unsignedLong
[Definition:]
unsignedLong is ·derived· from
nonNegativeInteger by setting the value of
·maxInclusive· to be 18446744073709551615.
The ·base type· of unsignedLong is
nonNegativeInteger.
3.3.21.1 Lexical representation
unsignedLong has a lexical representation consisting
of a finite-length sequence of decimal digits (#x30-#x39).
For example: 0,
12678967543233, 100000.
3.3.21.2 Canonical representation
The canonical representation for unsignedLong is defined
by prohibiting certain options from the
Lexical representation (§3.3.21.1). Specifically,
leading zeroes are prohibited.
3.3.22 unsignedInt
[Definition:]
unsignedInt is ·derived· from
unsignedLong by setting the value of
·maxInclusive· to be 4294967295. The
·base type· of unsignedInt is
unsignedLong.
3.3.22.1 Lexical representation
unsignedInt has a lexical representation consisting
of a finite-length
sequence of decimal digits (#x30-#x39). For example: 0,
1267896754, 100000.
3.3.22.2 Canonical representation
The canonical representation for unsignedInt is defined
by prohibiting certain options from the
Lexical representation (§3.3.22.1). Specifically,
leading zeroes are prohibited.
3.3.23 unsignedShort
[Definition:]
unsignedShort is ·derived· from
unsignedInt by setting the value of
·maxInclusive· to be 65535. The
·base type· of unsignedShort is
unsignedInt.
3.3.23.1 Lexical representation
unsignedShort has a lexical representation consisting
of a finite-length
sequence of decimal digits (#x30-#x39).
For example: 0,
12678, 10000.
3.3.23.2 Canonical representation
The canonical representation for unsignedShort is defined
by prohibiting certain options from the
Lexical representation (§3.3.23.1). Specifically, the
leading zeroes are prohibited.
3.3.23.4 Derived datatypes
The following ·built-in·
datatypes are ·derived· from
unsignedShort:
3.3.24 unsignedByte
[Definition:]
unsignedByte is ·derived· from
unsignedShort by setting the value of
·maxInclusive· to be 255. The
·base type· of unsignedByte is
unsignedShort.
3.3.24.1 Lexical representation
unsignedByte has a lexical representation consisting
of a finite-length
sequence of decimal digits (#x30-#x39).
For example: 0,
126, 100.
3.3.24.2 Canonical representation
The canonical representation for unsignedByte is defined
by prohibiting certain options from the
Lexical representation (§3.3.24.1). Specifically,
leading zeroes are prohibited.
3.3.25 positiveInteger
[Definition:]
positiveInteger is ·derived· from
nonNegativeInteger by setting the value of
·minInclusive· to be 1. This results in the standard
mathematical concept of the positive integer numbers.
The ·value space· of positiveInteger
is the infinite set {1,2,...}. The ·base type· of
positiveInteger is nonNegativeInteger.
3.3.25.1 Lexical representation
positiveInteger has a lexical representation consisting
of an optional positive sign ("+") followed by a finite-length
sequence of decimal digits (#x30-#x39).
For example: 1, 12678967543233, +100000.
3.3.25.2 Canonical representation
The canonical representation for positiveInteger is defined
by prohibiting certain options from the
Lexical representation (§3.3.25.1). Specifically, the
optional "+" sign is prohibited and leading zeroes are prohibited.